Come trovare l'angolo nel moto parabolico
Come si trova l'angolo nel moto parabolico? Ecco cos'è e quali sono le formule da applicare per svolgere gli esercizi di fisica sul moto del proiettile
Indice
Introduzione
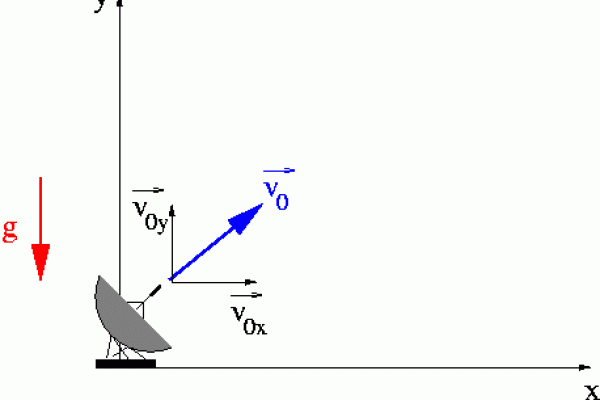
Il moto parabolico è bidimensionale e viene anche comunemente denominato "moto del proiettile" perché è facilmente descrivibile con la traiettoria che assume un proiettile sparato da un punto specifico fino a che lo stesso non tocchi terra.
In questa guida vediamo le formule da applicare per trovare l'angolo nel moto parabolico.
Occorrente
- Calcolatrice scientifica
- Foglio per trascrivere i calcoli e i vari passaggi
- Dimestichezza con la matematica e la fisica
La composizione
Il moto parabolico è la composizione di due differenti moti indipendenti e simultanei; il moto rettilineo uniforme, con velocità costante, che si svolge sull'asse "x" e quello che si svolge sull'asse "y" del sistema cartesiano denominato uniformemente decelerato (durante la fase di salita) e uniformemente accelerato (durante la fase di discesa).
Prima di partire con i calcoli diretti è necessario specificare alcuni dei simboli che andremo a utilizzare nelle formule seguenti.
Per calcolare l'angolo partiamo dalla formula che consente di calcolare la gittata (xG) e così facendo troviamo che: xG = 2vo^2 cos^2a tan a / g di cui xG = 2vo^2 cos a sin a / g fino ad arrivare a xG = vo^2 2cos a sin a / g. A questo punto è necessario utilizzare semplicemente le formule inverse per trovare l'angolo "α".
I termini
Con "xG" verrà indicato il termine per specificare la gittata, ovvero la distanza orizzontale tra il punto di lancio e il punto in cui il proiettile tocca il suolo.
Mentre "vo" è il vettore velocità del proiettile che in questo caso avrà un valore costante, "g" è il valore dell'accelerazione di gravità ed anche in questo caso rimane costante.
Il valore relativo all'angolo Alpha verrà indicato con l'utilizzo della lettera "α". Inoltre, nelle formule il simbolo "^" indica l'elevazione, mentre il numero successivo il valore (esempio: 2^2 significa 2 elevato al quadrato). Il simbolo "*" indica la moltiplicazione e il simbolo "/" indica la divisione.
Conclusione
Il primo passaggio è lo spostamento di "g" tramite la formula xG * g = vo^2 2cos α sin α. Ora portiamo anche "vo^2" e così facendo la formula diventerà xG * g / vo^2 = sin^2 α. A questo punto possiamo anche scrivere in questo modo la formula: sin2 α = g xG / vo^2. Abbiamo visto come trovare l'angolo nel moto parabolico.
Consigli
Alcuni link che potrebbero esserti utili:
- Come dimostrare il moto rettilineo uniforme
- Come risolvere un problema di fisica sul moto di un proiettile
- Fisica: la legge di conservazione della quantità di moto


